Beating the Odds: The Math of Shiny Hunting and an Implementation in Common Lisp

From generation 6 onward, the base odds of catching a shiny Pokemon is 1/4096. This includes Pokemon Brilliant Diamond, in which I recently acquired a shiny Arceus on my 1676th attempt at doing so. This feels decently lucky, and that's reflected in my disbelief at seeing the shiny on my screen when I was about to give up for the day and do something productive, but reasoning about these results in an interesting way requires doing some math. What follows is an attempt to explain how this math works, as I had to relearn it recently (I slept through almost all my statistics classes) to build an as-of-yet-not-released shiny hunting tool and want to solidify my understanding of it.

Since shiny Pokemon, as far as I am aware, do not exist in superposition and you either get one or you don't, we have a convenient building block to start our exploration with: the binomial distribution. To find the probability of getting exactly \(k\) shinies in \(n\) attempts with a probability of \(p\), we can use this formula:

\[ \binom{n}{k}p^{k}(1 - p)^{n - k} \]

The idea here is that there are \(n - k\) failed attempts, and each of those failed attempts has a probability of \(1 - p\) (that being \(1 - 1/4096 = 4095/4096\) in our case). We toss the probabilities of our failed attempts together along with our \(k\) successful attempts with a probability of \(p\), and we do a funky parenthetical thing. The purpose of the funky parenthetical thing, the binomial coefficient, often read as "n choose k," is that we care about the order these events occur in, i.e. we want to consider every combination of \(n\) attempts that would get us our \(k\) shinies. The binomial coefficient represents exactly that and works like so:

\[ \binom{n}{k} = \frac{n!}{k!(n - k)!} \]

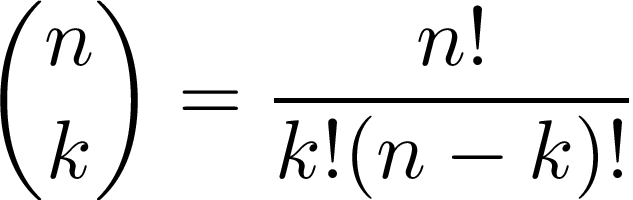
Since we can't replay an attempt twice, and we only care about exactly \(k\) successes, we're using factorials to calculate this. Shiny hunting is not catch-and-release.

To find the binomial coefficient, we first need a factorial function. I chose the following implementation:

(let ((memoized (make-hash-table)))
  (setf (gethash 0 memoized) 1)
  (setf (gethash 1 memoized) 1)
  (defun factorial (n)
    (nth-value 0 (or (gethash n memoized)
                     (setf (gethash n memoized)
                           (* n (factorial (1- n))))))))

I originally wrote a tail-recursive version, which was more performant for any given run provided the above function hadn't done any memoization yet, but we're going to be calling this function quite a lot and I'd like to avoid doing the same work more than once. I also decided I wanted a "repl mode" in this shiny hunting tool where a user can repeatedly press a key to increment the counter for the hunt they're on, so these memoized outputs should stick around in memory for a decent amount of time. A raw run with an n of about 25000 crashes on my machine, but that's an acceptable upper bounds for me. I did ponder an implementation that uses this memoized version unless we pass in an n greater than the highest memoized value by some threshold, when it will then run a tail-recursive version before memoizing the final output to be used as a new "anchor" memoized value, but that seems overkill for this project.

Armed with this, adding "n choose k" to our vocabulary is easy:

(defun binomial-coefficient (n k)
  (/ (factorial n) (* (factorial k) (factorial (- n k)))))

The next step is to simply hook our new function up to the rest of the formula:

(defun binomial-pmf (p n k)
  (* (binomial-coefficient n k)
     (expt p k)
     (expt (- 1 p) (- n k))))

Here pmf refers to the probability mass function and from what I can tell it's fancy math speak for what we've been talking about this whole time. When we execute it, we get this:

(binomial-pmf 1/4096 1676 1) ; 0.27182782

This tells us the probability of getting exactly 1 shiny in 1676 attempts, but what might be more interesting is the probability of getting at least 1 shiny in 1676 attempts; this will also compare our luck with people who for some reason attempted and succeeded at catching a shiny Arceus multiple times.

Since we can find the probability of exactly \(k\) shinies for \(n\) attempts, we can take the intuitive approach and sum the odds of getting 1 shiny in 1 attempt with the odds of getting 1 shiny in 2 attempts with the odds of getting 2 shinies in 2 attempts and so on. My strategy was to take an indirect approach and start by figuring out the probability of getting less than or equal to \(k\) shinies, and then use the inverse of that to reach our goal. It may not be the most efficient route, but it was the easiest for me to grok and didn't take long to build with the above functions.

We can write a beautiful little function to find the probability of getting \(\leq k\) shinies like so:

(defun binomial-cdf (p n k)
  (apply #'+ (loop for i from 0 to k collect (binomial-pmf p n i))))

With cdf meaning cumulative distribution function, since we're accumulating shiny Pokemon. In our case, all we have to do is sum the probability of getting 0 shinies with the probability of getting a single shiny, but I prefer the generalized solution. Naturally, this probability will be much higher than the probability of getting exactly 1 shiny:

(binomial-cdf 1/4096 1676 1) ; 0.9359895

To find the inverse, we do some subtraction:

(defun binomial-cdf-greater-or-equal (p n k)
  (+ (- 1 (binomial-cdf p n k)) (binomial-pmf p n k)))

Note that we add on the probability of getting exactly 1 shiny at the end; the inverse of the cumulative distribution function would only tell us the odds of getting > 1 shinies. I also feel like the name of this function betrays the elegance of its implementation.

We can finally see how lucky I was:

(binomial-cdf-greater-or-equal 1/4096 1676 1) ; 0.33583832

At 1676 tries with odds of 1/4096, you'd have a roughly 34% chance at getting at least 1 shiny. Not bad! Hopefully I stay lucky; if I get a little too unlucky I may have to refactor that factorial function.

This was a pretty fun programming side quest overall, and I got a tool that elucidates some interesting facts regarding this and potentially future shiny hunts out of it. Currently the program is pretty barebones and I've only been adding features to it as I need them (you currently cannot log a new shiny hunt in the sqlite database it's running on as I have not started a new shiny hunt since I caught my Arceus). When it reaches a state closer to what I would consider finished I'll likely edit this post with a link to the complete source code, although that might be sooner rather than later as my primary motivation for building my own tool was the lack of reasonable existing solutions.